无监督学习和流形学习 Unsupervised Learning & Manifold Learning
无监督学习和流形学习 Unsupervised Learning & Manifold Learning
The Elements of Statistical Learning Data Mining, Inference, and Prediction 一书第14章的笔记
监督学习和无监督学习 Supervised Learning & Unsupervised Learning
监督学习
给定输入\(X^T = (X_1, ..., X_p)\) 以预测一个或多个输出\(Y = (Y_1, ..., Y_m)\) 的值,这种方式通常被称作有监督学习。监督体现在真值与预测值的误差,即损失函数\(L(y, \hat{y})\),如 \(L(y, \hat{y}) = (y - \hat{y})^2\)。
具体的,若假设 \((X, Y)\) 是由联合概率密度\(Pr(X, Y)\) 表示的随机变量,有监督学习可以被形式化地描述为一个密度估计问题,重点在于确定条件密度\(Pr(Y|X)\) 的属性。
\[\mu(x) = \text{argmin}_\theta E_{Y|X}L(Y, \theta)\]
根据条件概率公式 \(Pr(X, Y) = Pr(Y|X) \cdot Pr(X)\),其中 \(Pr(X)\) 是仅 \(X\) 值的联合边缘密度。考虑输入维度通常较大,联合边缘密度 \(Pr(X)\) 会遭遇“维数灾难”,需要极大的样本量才能覆盖空间,而完整的条件密度 \(Pr(Y|X)\) 包含了 \(Y\) 在给定 \(X\) 时的所有统计信息,包括方差、偏度、多峰分布等复杂形状。有监督学习仅关注能够最小化误差的那个点,即条件期望\(\mu(x) = E[Y|X]\),从而将高维度的全概率分布估计问题转换为低维度的函数逼近问题。
无监督学习
在此情形下,我们拥有一组 \(N\) 个观测值 \((x_1, x_2, ..., x_N)\),它们来自具有联合密度 \(Pr(X)\) 的随机 p-维向量 \(X\)。其目标是在没有监督者或教师提供正确答案或误差程度的情况下,直接推断该概率密度的属性。与有监督学习相比,\(X\) 的维度有时要高得多,且感兴趣的属性往往比简单的位置估计更为复杂。
低维问题(例如 \(p \le 3\))中,存在多种有效的非参数方法可用于直接估计所有 \(X\) 值处的密度 \(Pr(X)\) 本身并进行图形化表示。由于维数灾难,这些方法在高维空间中会失效。因此,必须退而求其次,去估计较为粗略的全局模型(如高斯混合模型),或使用各种简单的描述性统计量来表征 \(Pr(X)\)。
针对高维数据,主要有以下几种方法:
- 流形学习与潜变量:主成分 (Principal Components,PCA)、多维缩放 (Multidimensional Scaling,MDS)、自组织映射 (Self-Organizing Maps,SOM) 和主曲线 (Principal Curves) 等方法,试图识别 \(X\) 空间中代表高数据密度的低维流形。
- 关联规则
- 聚类分析
这份笔记会简单设计关联规则和聚类分析,主要关注流形学习
关联规则
关联规则
关联规则寻找变量 \(X = (X_1, X_2, ..., X_p)\) 中在数据库内最频繁共同出现的联合值。
从广义上讲,关联规则的基本目标是为特征向量 \(X\) 寻找一组原型 \(X\) 值 \(v_1, ..., v_L\),使得在这些值处评估的概率密度 \(Pr(v_l)\) 相对较大。
购物车模型
考虑购物车模型,假设 \(X\) 是一个描述购物车的向量。如果有 10,000 种商品,这个空间就是 10,000 维的。每一个具体的“购物篮”(也就是每一个顾客的购买记录)就是这个空间里的一个点。\(Pr(v_l)\)代表了某个特定的点(即某种特定的商品组合)出现的频繁程度。如大多数商品组合是根本没人买的(比如“泻药 + 生日蛋糕 + 汽车轮胎”),这些地方的密度接近 0。而某些特定的组合(比如“牛奶 + 面包”)会有很多人购买,这些点在空间中会形成“高密度区域”。
项集
合取规则将目标简化为,寻找变量值的子集 \(s_1, ..., s_p\),使得每个变量同时取值于其各自子集内的概率相对较大:
\[Pr \left[ \bigcap_{j=1}^p (X_j \in s_j) \right]\]
对于购物车这种零一问题,子集 \(s_j\) 要么是 \(X_j\) 的单个值 \(v_{0j}\),要么是 \(X_j\) 的所有可能值 \(S_j\)(即该变量不参与规则)。问题转化为寻找一个整数子集 \(\mathcal{K} \subset \{1, ..., K\}\),使得以下概率较大:
\[Pr \left( \prod_{k \in \mathcal{K}} Z_k = 1 \right)\]
对于非零一问题,可以用中位数为界切分并编码为哑变量,也可以将有 \(k\) 个类别的分类变量,编码为 \(k\) 个哑变量。
集合 \(\mathcal{K}\) 被称为“项集”,其包含的变量数称为项集的“大小”。(相当于忽略项集外的元素)
项集 \(\mathcal{K}\) 的支持度 \(T(\mathcal{K})\) 估计为数据库中满足该合取的观测值比例
\[T(\mathcal{K}) = \frac{1}{N} \sum_{i=1}^N \prod_{k \in \mathcal{K}} z_{ik}\]
若观测值 \(i\) 满足 \(\prod_{k \in \mathcal{K}} z_{ik} = 1\),则称该观测“包含”项集 \(\mathcal{K}\)。可设定一个下限支持度 \(t\),寻找所有支持度大于该下限的项集 \(\{\mathcal{K}_l | T(\mathcal{K}_l) > t\}\)。
考虑任何项集 \(\mathcal{K}\) 的子集 \(L\) (\(L \subseteq \mathcal{K}\)) 的支持度必然大于或等于 \(\mathcal{K}\) 的支持度 (\(T(L) \ge T(\mathcal{K})\)),可以使用Apriori算法高效求解:
- 计算所有单项集 (Single-item sets) 的支持度,丢弃低于阈值 \(t\) 的项
- 利用第一遍留下的单项,生成所有可能的双项集 (Size-two item sets) 候选,计算支持度并过滤。
- 迭代:为了生成大小为 \(m\) 的频繁项集,仅考虑那些所有 \(m-1\) 大小的祖先项集都是频繁项集的候选者。
- 直到上一轮没有候选规则满足阈值。
关联规则
Apriori 算法返回的高支持度项集 \(\mathcal{K}\) 将被转化为关联规则:将 \(\mathcal{K}\) 划分为两个不相交的子集 \(A\) 和 \(B\) (\(A \cup B = \mathcal{K}\)),写作 \(A \Rightarrow B\)。其中 \(A\) 为前件 (Antecedent),\(B\) 为后件 (Consequent)。
定义
- 置信度:\(C(A \Rightarrow B) = \frac{T(A
\Rightarrow B)}{T(A)}\)
- 这可以看作是条件概率 \(Pr(B|A)\) 的估计。即在包含 \(A\) 的交易中,同时也包含 \(B\) 的比例。
- 提升度:\(L(A \Rightarrow B) = \frac{C(A
\Rightarrow B)}{T(B)}\)
- 这是对关联度量 \(\frac{Pr(A \text{ and } B)}{Pr(A)Pr(B)}\) 的估计。它衡量了 \(A\) 的出现将 \(B\) 的概率提升了多少(相对于 \(B\) 的无条件概率)。
最终输出是满足支持度阈值 \(t\) 和置信度阈值 \(c\) 的所有规则的集合。
将无监督学习转化为有监督学习
通过引入一个已知的参考分布 (Reference Density) \(g_0(x)\),将估计未知数据密度 \(g(x)\) 的问题转化为区分真实数据与参考数据的分类问题。
取 \(N\) 个真实样本 \(x_i \sim g(x)\),标记为 \(Y=1\)。利用蒙特卡洛方法生成 \(N_0\) 个参考样本 \(\sim g_0(x)\),标记为 \(Y=0\)。在混合数据集上训练一个分类器(如逻辑回归),估计条件概率 \(\mu(x) = E(Y|x) = Pr(Y=1|x)\)。
由此可以反推密度,根据贝叶斯公式,未知密度 \(g(x)\) 可由下式估计:
\[\hat{g}(x) = g_0(x) \frac{\hat{\mu}(x)}{1 - \hat{\mu}(x)}\]
可以使用不同的参考分布选择策略决定分析关注的类型:
- 均匀分布:用于发现数据中的高密度区域(聚类或模式)
- 高斯分布:用于检测数据偏离正态分布的程度
- 边缘密度乘积:
- \(g_0(x) = \prod_{j=1}^p g_j(x_j)\),用于检测变量间的独立性偏离,此类样本可通过在各变量内部独立置换数据顺序来生成。
广义关联规则
目标是寻找变量子集 \(J\) 和对应的取值区间 \(s_j\),使得广义项集 \(\{(X_j \in s_j)\}_{j \in J}\) 的联合概率(支持度)显著较大:
\[Pr \left( \bigcap_{j \in J} (X_j \in s_j) \right) \text{ is large}\]
与传统购物篮分析不同,这里的 \(s_j\) 可以是连续变量的区间或分类变量的集合。
传统关联规则(基于均匀分布参考)倾向于发现那些由本身频率就很高的单项组成的规则。如“面包”和“牛奶”本身很畅销,它们的组合支持度自然很高;伏特加 \(\Rightarrow\) 鱼子酱,虽然二者关联性极强(提升度高),但因为鱼子酱本身极其稀有,导致该规则的联合支持度很低,容易被基于支持度阈值的算法(如 Apriori)过滤掉。
使用边缘密度乘积作为参考分布 \(g_0(x)\),任何被检测出的高密度区域(\(g(x) \gg g_0(x)\))都纯粹反映了变量间的关联性,而非变量自身的流行度。这使得像“伏特加 \(\Rightarrow\) 鱼子酱”这样的强关联但低频的规则有机会浮出水面。
- 选择参考分布(如边缘密度乘积)并生成参考样本。
- 构建有监督学习问题(真实数据 vs. 参考数据)。
- 寻找目标函数 \(\mu(x)\)
相对较大的区域 \(R\)
- \[R = \bigcap_{j \in J} (X_j \in s_j)\]
1 |
|
聚类分析
聚类分析,亦称数据分割 (Data Segmentation),其核心目标是将一组对象分组或分割成若干子集或“簇 (Clusters)”,使得同一簇内的对象彼此之间的关联度高于不同簇的对象。
K-均值算法是一种自顶向下的程序,通过以下步骤迭代直至收敛: - 猜测簇中心的初始位置。 - 将每个数据点分配给最近的簇中心(欧几里得距离)。 - 将每个簇中心替换为该簇内所有数据点的坐标均值
邻近度和相异度
数据可以直接以对象对之间的邻近度(相似性或亲和力)的形式呈现,这些数据可以是相似度,也可以是相异度(差异或缺乏亲和力)。此类数据由一个 \(N \times N\) 矩阵 \(D\) 表示,其中 \(N\) 是对象数量,元素 \(d_{ii'}\) 记录了第 \(i\) 个和第 \(i'\) 个对象之间的邻近度。
使用p个属性值的临近度矩阵即可表现观测值之间的“距离”:
\[D(x_i, x_{i'}) = \sum_{j=1}^p d_j(x_{ij}, x_{i'j})\]
最常见的选择是平方距离 (Squared Distance):\(d_j(x_{ij}, x_{i'j}) = (x_{ij} - x_{i'j})^2\)。
聚类也可以基于相关性:
\[\rho(x_i, x_{i'}) = \frac{\sum_j (x_{ij} - \bar{x}_i)(x_{i'j} - \bar{x}_{i'})}{\sqrt{\sum_j (x_{ij} - \bar{x}_i)^2 \sum_j (x_{i'j} - \bar{x}_{i'})^2}}\]
注意这是对变量而非观测值求平均。如果观测值首先被标准化,那么 \(\sum_j (x_{ij} - x_{i'j})^2 \propto 2(1 - \rho(x_i, x_{i'}))\),基于相关性的聚类等价于基于平方距离的聚类。
对于叙述变量,可以将原始值替换为以下值来定义:
\[\frac{i - 1/2}{M}, i=1, \dots, M \]
对于分类变量,通常使用零一矩阵。
加权平均策略
将 \(p\) 个单独属性的相异度合并为单一的总体相异度 \(D(x_i, x_{i'})\) 通常通过加权平均(凸组合)实现:
\[D(x_i, x_{i'}) = \sum_{j=1}^p w_j \cdot d_j(x_{ij}, x_{i'j}); \quad \sum_{j=1}^p w_j = 1\]
权重 \(w_j\) 调节第 \(j\) 个变量在决定整体相异度时的相对影响力。将每个变量的权重设为相同(如 \(w_j=1\))并不意味着所有属性具有相同的影响力。
- 第 \(j\) 个属性的影响力取决于其在所有数据对上的平均相异度 \(\bar{d}_j\)。
- 第 \(j\) 个变量的相对影响力实际上是 \(w_j \cdot \bar{d}_j\)。
- 若要使所有属性具有相同影响力,应设定 \(w_j \sim 1/\bar{d}_j\)。对于平方欧几里得距离,这意味着权重与变量的方差成反比(即标准化变量)。
对于定量变量和平方误差距离: \[D_I(x_i, x_{i'}) = \sum_{j=1}^p w_j \cdot (x_{ij} - x_{i'j})^2 \]
此时平均距离:
\[\bar{d}_j = \frac{1}{N^2} \sum_{i=1}^N \sum_{i'=1}^N (x_{ij} - x_{i'j})^2 = 2 \cdot \text{var}_j\]
其中 \(\text{var}_j\) 是 \(\text{Var}(X_j)\) 的样本估计。因此,每个变量的相对重要性与其方差成正比。
聚类算法
聚类算法主要分为三种不同的类型:
组合算法:直接在观测数据上工作,不直接参考底层的概率模型。
混合建模:假设数据是来自某个由概率密度函数描述的总体的独立同分布 (i.i.d) 样本。该密度函数被特征化为一个参数化模型,由分量密度函数的混合组成;每个分量密度描述一个簇。该模型随后通过最大似然或相应的贝叶斯方法拟合到数据上。
寻找模式:采取非参数视角,试图直接估计概率密度函数的不同模式 (modes)。最接近各个模式的观测值随后定义了单独的簇。
组合算法
最流行的聚类算法直接将每个观测值分配给一个组或簇,而不考虑描述数据的概率模型。
每个观测值由整数 \(i \in \{1, \dots, N\}\) 唯一标记。预先设定簇的数量 \(K < N\),每个簇由整数 \(k \in \{1, \dots, K\}\) 标记。每个观测值被分配给唯一的一个簇。这些分配可以用一个多对一的映射或编码器 \(k = C(i)\) 来表征,它将第 \(i\) 个观测值分配给第 \(k\) 个簇。
既然目标是将相近的点分配给同一个簇,一个自然的损失(或“能量”)函数是:
\[W(C) = \frac{1}{2} \sum_{k=1}^K \sum_{C(i)=k} \sum_{C(i')=k} d(x_i, x_{i'})\]
表征了分配给同一簇的观测值彼此接近的程度。
这种散度可以被理解为簇内散度,考虑总散度:
\[T = \frac{1}{2} \sum_{i=1}^N \sum_{i'=1}^N d_{ii'} = \frac{1}{2} \sum_{k=1}^K \sum_{C(i)=k} \left( \sum_{C(i')=k} d_{ii'} + \sum_{C(i') \neq k} d_{ii'} \right) = W(C)+B(C)\]
以及簇间散度:
\[B(C) = \frac{1}{2} \sum_{k=1}^K \sum_{C(i)=k} \sum_{C(i') \neq k} d_{ii'}\]
剩余的部分,即刚刚的\(W(C)\):
\[W(C) = T - B(C)\]
考虑划分方式是一个组合问题,此类可行策略通常需要结合贪婪策略:
指定一个初始划分。
在每个迭代步骤中,以某种方式改变簇分配,使得标准的值比前一个值有所改进。
此类聚类算法的区别在于它们在每次迭代中修改簇分配的规定。
当规定无法提供改进时,算法终止,并将当前分配作为其解。 这些算法收敛于局部最优 (local optima),与全局最优相比,这可能是高度次优的。
K-means算法
它专门用于所有变量均为定量类型的情况,并选择平方欧几里得距离作为相异度度量:
\[d(x_i, x_{i'}) = \sum_{j=1}^p (x_{ij} - x_{i'j})^2 = ||x_i - x_{i'}||^2\]
簇内散度写作:
\[W(C) = \frac{1}{2} \sum_{k=1}^K \sum_{C(i)=k} \sum_{C(i')=k} ||x_i - x_{i'}||^2 = \sum_{k=1}^K N_k \sum_{C(i)=k} ||x_i - \bar{x}_k||^2\]
1 |
|
流形学习
主成分
主成分通常被呈现为近似一组 \(N\) 个点 \(x_i \in \mathbb{R}^p\) 的线性流形。
如果 \(V\) 是 \(\mathbb{R}^p\) 中的一个 \(q\) 维线性子空间,那么线性流形 \(M\) 可以表示为:
\[M = x_0 + V = \{ x_0 + v \mid v \in V \}\]
线性近似模型为一组 \(\mathbb{R}^p\) 中数据的主成分提供了一系列秩 (rank) \(q \le p\) 的最佳线性近似。 记观测值为 \(x_1, x_2, \dots, x_N\),考虑用于表示它们的秩 \(q\) 线性模型:
\[f(\lambda) = \mu + \mathbf{V}_q \lambda\]
其中:\(\mu\) 是 \(\mathbb{R}^p\) 中的位置向量;\(\mathbf{V}_q\) 是一个 \(p \times q\) 的矩阵,包含 \(q\) 个正交单位向量作为列;\(\lambda\) 是一个 \(q\) 维参数向量。
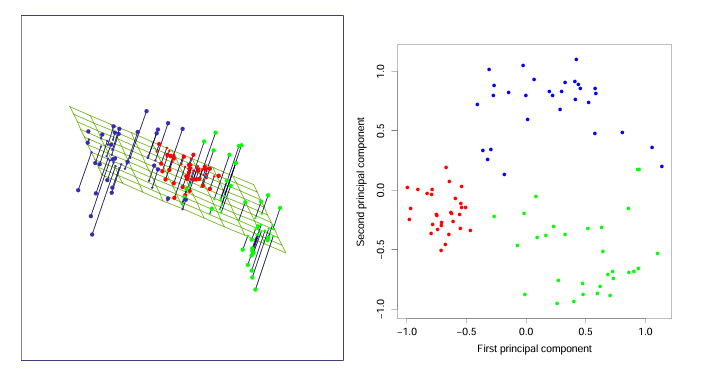
几何上,将原始的 \(p\) 维数据点 \(x_i\) 投影到 \(q\) 维空间,得到坐标 \(\lambda_i\);然后使用模型 \(f(\lambda_i)\) 将其还原回 \(p\) 维空间。\(x_i\) 与 \(f(\lambda_i)\) 之间的距离,就是所谓的“信息损失”或“重构误差”。
通过最小二乘法拟合该模型等同于最小化重建误差:
\[\min_{\mu, \{\lambda_i\}, \mathbf{V}_q} \sum_{i=1}^N ||x_i - \mu - \mathbf{V}_q \lambda_i||^2\]
我们可以针对 \(\mu\) 和 \(\lambda_i\) 进行部分优化以获得:
\[\hat{\mu} = \bar{x}\]
\[\hat{\lambda}_i = \mathbf{V}_q^T (x_i - \bar{x})\]
问题转化为寻找正交矩阵:
\[\min_{\mathbf{V}_q} \sum_{i=1}^N ||(x_i - \bar{x}) - \mathbf{V}_q \mathbf{V}_q^T (x_i - \bar{x})||^2\]
其中,\(p \times p\) 矩阵 \(\mathbf{H}_q = \mathbf{V}_q \mathbf{V}_q^T\) 是一个投影矩阵,它将每个点 \(x_i\) 映射到其秩 \(q\) 的重建版本 \(\mathbf{H}_q x_i\) 上,即 \(x_i\) 在由 \(\mathbf{V}_q\) 列张成的子空间上的正交投影。
对于\(N\times p\)的中心化(假设每一列均值都为0,因此不用考虑流形的中心)数据矩阵,对X进行奇异值分解,得到:
\[\mathbf{X} = \mathbf{U} \mathbf{D} \mathbf{V}^T\]
其中,\(\mathbf{U}\) 是 \(N \times p\) 的正交矩阵 (\(\mathbf{U}^T \mathbf{U} = \mathbf{I}_p\)),其列 \(\mathbf{u}_j\) 称为左奇异向量 (left singular vectors);\(\mathbf{V}\) 是 \(p \times p\) 的正交矩阵 (\(\mathbf{V}^T \mathbf{V} = \mathbf{I}_p\)),其列 \(v_j\) 称为右奇异向量 (right singular vectors);\(\mathbf{D}\) 是 \(p \times p\) 的对角矩阵,对角元素 \(d_1 \ge d_2 \ge \dots \ge d_p \ge 0\) 称为奇异值 (singular values)。
例如, \[\mathbf{X} = \begin{pmatrix} 2 & 2 & 0.1 \\ -2 & -2 & -0.1 \\ 1 & 1 & 0 \\ -1 & -1 & 0 \end{pmatrix}_{(4 \times 3)}\] 分解后得到: \[\mathbf{D} = \begin{pmatrix} 4.472 & 0 & 0 \\ 0 & 0.141 & 0 \\ 0 & 0 & 0 \end{pmatrix}\] \(d_1 = 4.472\):这是主信号的强度。它非常大,说明数据主要沿着第一个方向延伸。 \[\mathbf{V}^T = \begin{pmatrix} 0.707 & 0.707 & 0.022 \\ -0.016 & -0.016 & 0.999 \\ -0.707 & 0.707 & 0 \end{pmatrix}\] $ [0.707, 0.707, 0]\(是主信号的方向,\) [0, 0, 1]\(是z轴方向的扰动的方向\)\(\mathbf{U} = \begin{pmatrix} -0.633 & 0.707 & 0 & \dots \\ 0.633 & 0.707 & 0 & \dots \\ -0.316 & 0 & 0 & \dots \\ 0.316 & 0 & 0 & \dots \end{pmatrix}_{(4 \times 4)}\)$ 第一列 \(u_{\cdot 1}\)描述了 4 个样本在第一主成分的分布模式。 样本 1 (\(x_1=[2,2,0.1]\)):对应 \(u_{1,1} = -0.633\)。绝对值最大,说明它离中心最远。样本 2 (\(x_2=[-2,-2,-0.1]\)):对应 \(u_{2,1} = 0.633\)。与样本 1 对称,方向相反。样本 3 (\(x_3=[1,1,0]\)):对应 \(u_{3,1} = -0.316\)。大小约为样本 1 的一半。样本 4 (\(x_4=[-1,-1,0]\)):对应 \(u_{4,1} = 0.316\)。与样本 3 对称。 注意,因为p = 3,我们只关注前3行。 前述的参数\(\lambda\)即为\(\mathbf{U} \cdot \mathbf{D}\) 的前 \(q\) 列。 如果我们取 \(q=1\) \[\lambda= \mathbf{u}_1 \cdot d_1 = \begin{pmatrix} -0.633 \\ 0.633 \\ -0.316 \\ 0.316 \end{pmatrix} \times 4.472 \approx \begin{pmatrix} -2.83 \\ 2.83 \\ -1.41 \\ 1.41 \end{pmatrix}\]
主曲线和主曲面
主曲线是对主成分直线的推广,它为 \(\mathbb{R}^p\) 中的数据集提供了一条平滑的一维曲线近似。主曲面则更为一般,提供维度为 2 或更高的弯曲流形近似。
设 \(f(\lambda)\) 是 \(\mathbb{R}^p\) 中的一条参数化平滑曲线,\(\lambda\) 为参数(例如弧长)。对于每个数据值 \(x\),设 \(\lambda_f(x)\) 定义了曲线上距离 \(x\) 最近的点。 如果满足以下条件,则称 \(f(\lambda)\) 为随机向量 \(X\) 分布的主曲线:
\[f(\lambda) = E(X | \lambda_f(X) = \lambda)\]
即 \(f(\lambda)\) 是所有投影到该点的数据点的平均值。
主点以引入主曲线
考虑分布支撑集上的 \(k\) 个原型。对于每个点 \(x\),识别最近的原型。这将特征空间划分为了 Voronoi 区域。
Voronoi 区域 \(R_k\) 定义为特征空间中所有满足以下条件的点 \(x\) 的集合:点 \(x\) 到 \(\mu_k\) 的距离比到其他任何 \(\mu_j\) (\(j \neq k\)) 的距离都要近(或相等)。
最小化 \(X\) 到其原型的期望距离的 \(k\) 个点被称为分布的主点。每个主点都是自相容的,即它等于其 Voronoi 区域内 \(X\) 的均值(类似于 K-均值聚类发现的质心)。
主曲线可以被视为 \(k = \infty\) 的主点,但被约束为位于一条平滑曲线上。这类似于 SOM 将 K-均值聚类中心约束在一个平滑流形上。
1 | Principal Curve Algorithm |
主曲面
主曲面与主曲线形式完全相同,只是维度更高。最常用的是具有坐标函数 \(f(\lambda_1, \lambda_2)\) 的二维主曲面。
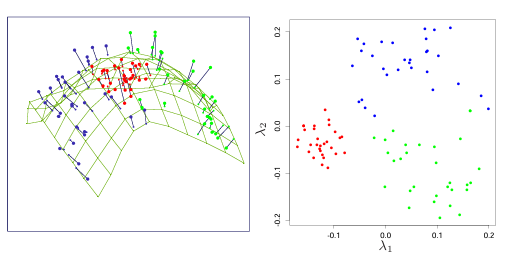
谱聚类
谱聚类的起点是所有观测对之间的 \(N \times N\) 成对相似度矩阵 \(s_{ii'} \ge 0\)。 我们将观测值表示为无向相似度图 (similarity graph) \(G = \langle V, E \rangle\) 的顶点 \(v_i\)。如果两个顶点的相似度为正(或超过某个阈值),则用边连接它们,边的权重由 \(s_{ii'}\) 给出。 聚类问题现在被重新表述为图划分 (graph-partition) 问题:我们希望划分图,使得不同组之间的边权重较低,而组内的边权重较高。
由相似度图的边权重组成的矩阵 \(\mathbf{W} = \{w_{ii'}\}\);另顶点 \(i\) 的度定义为 \(g_i = \sum_{i'} w_{ii'}\),即连接到它的边的权重之和。其中\(\mathbf{G}\) 是对角元素为 \(g_i\) 的对角矩阵。
图拉普拉斯矩阵 (Graph Laplacian)定义为\[\mathbf{L} = \mathbf{G} - \mathbf{W}\]。
谱聚类寻找对应于 \(\mathbf{L}\) 的 \(m\) 个最小特征值的 \(m\) 个特征向量 \(\mathbf{Z}_{N \times m}\),使用标准方法(如 K-均值)对 \(\mathbf{Z}\) 的行进行聚类,从而得到原始数据点的聚类结果。
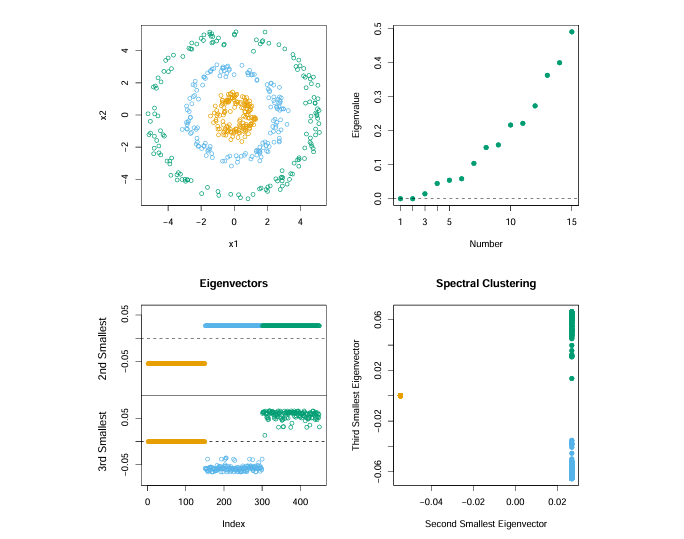
相当于,先投影再聚类。
核主成分分析 Kernel Principal Components
数据矩阵 \(\mathbf{X}\) 的主成分变量 \(\mathbf{Z}\) 可以直接从内积 (Gram) 矩阵 \(\mathbf{K} = \mathbf{X}\mathbf{X}^T\) 计算得出。
\[\tilde{\mathbf{K}} = (\mathbf{I} - \mathbf{M})\mathbf{K}(\mathbf{I} - \mathbf{M}) = \mathbf{U}\mathbf{D}^2\mathbf{U}^T\]
其中 \(\mathbf{M} = \mathbf{1}\mathbf{1}^T/N\),相当于减去行列的均值。
主成分为 \(\mathbf{Z} = \mathbf{U}\mathbf{D}\)。
PCA 简单地模仿了上述过程,但将核矩阵 \(\mathbf{K} = \{K(x_i, x_{i'})\}\) 解释为隐式特征 \(\langle \phi(x_i), \phi(x_{i'}) \rangle\) 的内积矩阵,并寻找其特征向量。
第 \(m\) 个主成分 \(\mathbf{z}_m\)(\(\mathbf{Z}\) 的第 \(m\) 列)的元素可以写为(忽略中心化):
\[z_{im} = \sum_{j=1}^N \alpha_{jm} K(x_i, x_j)\]
\(\alpha_{jm} = u_{jm}/d_m\)
具体来说,以高斯径向基核为例,假设我们有两个标量数据点 \(x, y \in \mathbb{R}\),,核函数定义为:
\[K(x, y) = \exp(-\gamma (x - y)^2)\]
将其展开:
\[K(x, y) = \exp(-\gamma (x^2 + y^2 - 2xy)) = \exp(-\gamma x^2) \exp(-\gamma y^2) \exp(2\gamma xy)\]
其中最后一项可以展开为无穷级数:
\[\exp(2\gamma xy) = \sum_{n=0}^{\infty} \frac{(2\gamma xy)^n}{n!} = \sum_{n=0}^{\infty} \left( \sqrt{\frac{(2\gamma)^n}{n!}} x^n \right) \left( \sqrt{\frac{(2\gamma)^n}{n!}} y^n \right)\]
现在,和函数可以协作两个向量的内积\(\phi(x)^T \phi(y)\):
\[K(x, y) = \sum_{n=0}^{\infty} \underbrace{\left( e^{-\gamma x^2} \sqrt{\frac{(2\gamma)^n}{n!}} x^n \right)}_{\phi(x)_n} \underbrace{\left( e^{-\gamma y^2} \sqrt{\frac{(2\gamma)^n}{n!}} y^n \right)}_{\phi(y)_n}\]
为了让等式成立,映射函数 \(\phi(x)\) 必须包含 \(x^0, x^1, x^2, x^3, \dots, x^\infty\) 所有阶项。 这意味着映射后的向量 \(\phi(x)\) 长这个样子:
\[\phi(x) = \left[ \dots, x, x^2, x^3, \dots, x^n, \dots \right]^T\]
有无数个分量。因此,特征空间是无限维的。它包含了 \(x\) 的所有次幂(\(x^1, x^2, \dots, x^\infty\)),这意味着它实际上通过所有可能的多项式组合来拟合数据。
因为 \(\mathcal{F}\) 可能是无限维的,我们通常无法直接写出 \(\mathbf{w}\) 的坐标。
想象 \(\mathbf{w}\) 是高维空间里的一个“标尺”,\(\langle \mathbf{w}, \phi(x) \rangle\) 就是计算向量 \(\phi(x)\)在这个标尺上的投影长度,即数据点\(x\)的主成分得分。内积的结果是一个标量。
在高维特征空间 \(\mathcal{F}\) 中找到一个主成分方向向量 \(\mathbf{w}\),这个 \(\mathbf{w}\) 一定位于所有训练数据 \(\phi(x_1), \dots, \phi(x_N)\) 张成的子空间里:
\[\mathbf{w} = \sum_{i=1}^{N} \alpha_i \phi(x_i)\]
尽管\(\phi(x)\)是无穷维度的,但因为训练数据有限,\(\alpha_i\)是有限的,目标转化为找到最优的\(\alpha\)。
根据投影的定义,第 \(i\) 个数据点 \(x_i\) 的坐标 \(z_i\) 是它与主成分方向 \(\mathbf{w}\) 的内积:
\[z_i = \langle \mathbf{w}, \phi(x_i) \rangle\]
即
\[z_i = \left\langle \sum_{j=1}^{N} \alpha_j \phi(x_j), \quad \phi(x_i) \right\rangle = \sum_{j=1}^{N} \alpha_j \underbrace{\langle \phi(x_j), \phi(x_i) \rangle}_{K_{ji}}\]
故有:
\[z_i = \sum_{j=1}^{N} K_{ji} \alpha_j\]
即开始处写下的公式,记作\(z = K\alpha\)。
只要知道了系数 \(\boldsymbol{\alpha}\),左乘一个核矩阵 \(\mathbf{K}\),就能得到坐标 \(\mathbf{z}\)。
在过程中,我们找到一种\(\boldsymbol{\alpha}\),使得投影后的方差最大。
\[\text{Var} = \|\mathbf{z}\|^2 = \mathbf{z}^T \mathbf{z} = (\mathbf{K} \boldsymbol{\alpha})^T (\mathbf{K} \boldsymbol{\alpha}) = \boldsymbol{\alpha}^T \mathbf{K}^T \mathbf{K} \boldsymbol{\alpha}\]
因为 \(\mathbf{K}\) 是对称的 (\(\mathbf{K}^T = \mathbf{K}\)),所以:
\[\text{Objective} = \boldsymbol{\alpha}^T \mathbf{K}^2 \boldsymbol{\alpha}\]
我们限制 \(\mathbf{w}\) 为单位向量 (\(\|\mathbf{w}\|^2 = 1\)),这等价于:
\[\text{Constraint}: \boldsymbol{\alpha}^T \mathbf{K} \boldsymbol{\alpha} = 1\]
问题转化为一个带约束的优化问题: - 目标:最大化 \(\boldsymbol{\alpha}^T \mathbf{K}^2 \boldsymbol{\alpha}\) - 约束:\(\boldsymbol{\alpha}^T \mathbf{K} \boldsymbol{\alpha} = 1\)
构造拉格朗日函数 \(L\)。引入一个乘子 \(\lambda\): \[L(\boldsymbol{\alpha}, \lambda) = \underbrace{\boldsymbol{\alpha}^T \mathbf{K}^2 \boldsymbol{\alpha}}_{\text{目标}} - \lambda (\underbrace{\boldsymbol{\alpha}^T \mathbf{K} \boldsymbol{\alpha} - 1}_{\text{约束}})\]
为了找到极值点,对 \(\boldsymbol{\alpha}\) 求导,并令导数为 0。
\[\frac{\partial L}{\partial \boldsymbol{\alpha}} = 2 \mathbf{K}^2 \boldsymbol{\alpha} - 2 \lambda \mathbf{K} \boldsymbol{\alpha}\]
令导数为 0:
\[2 \mathbf{K}^2 \boldsymbol{\alpha} - 2 \lambda \mathbf{K} \boldsymbol{\alpha} = 0\]
得到:
\[\mathbf{K}^2 \boldsymbol{\alpha} = \lambda \mathbf{K} \boldsymbol{\alpha}\]
这就意味着向量 \(\mathbf{K} \boldsymbol{\alpha}\) 必须是矩阵 \(\mathbf{K}\) 的特征向量。或者更直接地,如果矩阵 \(\mathbf{K}\) 是可逆的,可以两边同时“去掉”一个 \(\mathbf{K}\)(左乘 \(\mathbf{K}^{-1}\)):
\[\mathbf{K} \boldsymbol{\alpha} = \lambda \boldsymbol{\alpha}\]
即, \(\boldsymbol{\alpha}\) 的方向就是核矩阵 \(\mathbf{K}\) 的特征向量方向。
虽然 \(\boldsymbol{\alpha}\) 和 \(\mathbf{u}\) 方向一致,但它们的长度不同。设 \(\boldsymbol{\alpha} = c \mathbf{u}\),需要满足 \(\|\mathbf{w}\| = 1\):
\[\|\mathbf{w}\|^2 = \langle \mathbf{w}, \mathbf{w} \rangle = \boldsymbol{\alpha}^T \mathbf{K} \boldsymbol{\alpha} = 1\]
\[(c \mathbf{u})^T \mathbf{K} (c \mathbf{u}) = c^2 \mathbf{u}^T (\mathbf{K} \mathbf{u}) = 1\]
\[c^2 \mathbf{u}^T (\lambda \mathbf{u}) = c^2 \lambda \underbrace{(\mathbf{u}^T \mathbf{u})}_{=1} = 1\]
解得缩放系数 \(c = \frac{1}{\sqrt{\lambda}}\)。
代入:
\[\mathbf{z} = \mathbf{K} \left( \frac{\mathbf{u}}{\sqrt{\lambda}} \right)\]
由\(\mathbf{K} \mathbf{u} = \lambda \mathbf{u}\):
\[\mathbf{z} = \frac{\lambda}{\sqrt{\lambda}} \mathbf{u} = \sqrt{\lambda} \mathbf{u}\]
\(\mathbf{u}\) 是 \(\mathbf{K}\) 的第 \(k\) 个特征向量(SVD 中的 \(\mathbf{U}\) 的列)。\(\sqrt{\lambda}\) 是特征值的平方根(SVD 中的奇异值 \(d\))。
如果把前 \(m\) 个主成分并排放在一起:
左边变成坐标矩阵 \(\mathbf{Z}\);右边变成特征向量矩阵 \(\mathbf{U}\) 乘以 奇异值对角矩阵 \(\mathbf{D}\)(对角线上是 \(\sqrt{\lambda_1}, \sqrt{\lambda_2}, \dots\));得到:
\[\mathbf{Z} = \mathbf{U} \mathbf{D}\]
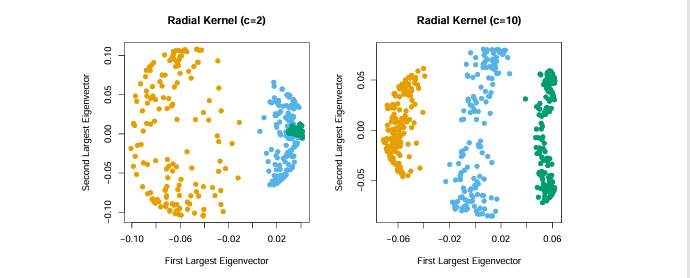
独立成分分析 ICA
独立成分分析 (ICA) 模型的形式为 \(X = \mathbf{A}S\),假设潜在变量 \(S_\ell\) 是统计独立。
其中S是源信号、A是混合过程,X是观测道德数据。
ICA 的目标是找到一个解混矩阵\(\mathbf{W}\),使得\(S \approx Y = \mathbf{W}X\)。
假设X已经白化、即\(Cov(X) = I\),由于S的协方差也是单位矩阵,A一定是正交的。因此,求解ICA问题就变成了寻找正交矩阵A,使得向量随机变量\(S = \mathbf{A}^T X\) 的分量是独立(且非高斯)的。
简单来说,许多独立的非高斯随机变量混合后的结果会越来越接近高斯分布,即中心极限定理。如此,解混就应该让数据变得更“不像”高斯分布。因此ICA也无法处理高斯信号。
引入熵的定义\(H(Y) = - \int g(y) \log g(y) dy\),根据信息论,在所有具有相等方差的随机变量中,高斯变量具有最大的熵。
引入互信息定义:
\[I(Y) = \sum_{j=1}^p H(Y_j) - H(Y)\]
即:随机向量 \(Y\) 的分量之间的依赖性的自然度量,也被称为密度 \(g(y)\) 与其独立版本 \(\prod g_j(y_j)\) 之间的 Kullback-Leibler 距离。
由此,ICA的目标进一步被表述为最小化 \(I(Y) = I(\mathbf{A}^T X)\) 。这等价于最小化各分量熵的和 \(\sum H(Y_j)\),也就是最大化各分量偏离高斯分布的程度。
也可以使用负熵来度量非高斯性:
\[J(Y_j) = H(Z_j) - H(Y_j)\]
其中 \(Z_j\) 是与 \(Y_j\) 同方差的高斯变量。负熵非负,主要衡量 \(Y_j\) 偏离高斯性的距离。
多维缩放 MDS
MDS 是一组核心的降维和可视化技术,与 ISOMAP 或 LLE 不同,MDS 的出发点不是保持某种局部邻域结构,而是在低维空间中尽可能保留样本之间的成对距离(或相似性)。
MDS 的核心目标是将高维数据(或样本间的距离矩阵)映射到低维空间(通常 \(d=2\) 或 \(3\)),使得低维空间中两点间的欧几里得距离 \(||z_i - z_j||\) 尽可能接近原始空间中的距离 \(d_{ij}\)。
经典多维缩放 (Classical MDS / PCoA)
通常称为主坐标分析 (Principal Coordinate Analysis, PCoA)。当使用欧几里得距离时,它等价于 PCA。
通过最小化“应变 (Strain)”损失函数来寻找低维坐标。它假设原始距离矩阵是欧几里得距离,并利用特征值分解得到闭式解 (Closed-form solution)。
具体通过, - 计算 \(N\) 个样本两两之间的距离矩阵 \(\mathbf{D} \in \mathbb{R}^{N \times N}\),其中 \(d_{ij}\) 是第 \(i\) 和第 \(j\) 个样本的距离。 - 构建双中心矩阵 (Double Centering): 首先计算距离的平方矩阵 \(\mathbf{D}^{(2)}\)(即每个元素是 \(d_{ij}^2\))。然后应用双中心化操作得到 Gram 矩阵 \(\mathbf{B}\): \[\mathbf{B} = -\frac{1}{2} \mathbf{J} \mathbf{D}^{(2)} \mathbf{J}\] - 其中 \(\mathbf{J} = \mathbf{I} - \frac{1}{N}\mathbf{1}\mathbf{1}^T\) 是中心化矩阵(\(\mathbf{I}\) 是单位矩阵,\(\mathbf{1}\) 是全1向量)。 这一步的作用是将距离矩阵转换为内积矩阵,即 \(b_{ij} \approx x_i^T x_j\)。 - 特征分解: 对矩阵 \(\mathbf{B}\) 进行特征值分解:\(\mathbf{B} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^T\)。 - 特征分解: 对矩阵 \(\mathbf{B}\) 进行特征值分解:\(\mathbf{B} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^T\)。 \[\mathbf{Z} = \mathbf{V}_d \mathbf{\Lambda}_d^{1/2}\]
等距特征映射 ISOMAP &局部线性嵌入 LLE
等距特征映射为每个数据点找到其邻居(欧几里得距离内的点)。构建图,邻居之间有边连接。任意两点间的测地线距离通过图上的最短路径近似。最后,将经典缩放应用于图距离,产生低维映射。
具体来说,对于每一个数据点 \(x_i\),确定其邻居。通常使用 \(K\)-近邻 (\(K\)-Nearest Neighbors) 或 \(\epsilon\)-半径球 ($ $-radius) 方法。在邻居之间建立连接边,边的权重设为两点间的欧几里得距离 \(d_E(x_i, x_j)\)。此时,数据被表示为一个加权图
对于图中任意两个非邻居点,通过图上的最短路径来近似它们之间的测地线距离,可以使用Dijkstra 算法。
将步骤 2 得到的测地线距离矩阵 \(D_G\) 作为输入,应用经典的 MDS 算法。通过特征分解,找到低维坐标 \(Y\),使得低维空间中的欧几里得距离尽可能逼近高维流形上的测地线距离。
局部线性嵌入为每个数据点由其邻近点的线性组合近似。然后构建一个低维表示,以此最好地保留这些局部近似。
如果流形在局部是平滑的,那么每一个数据点及其邻居大致位于一个局部的线性斑块上。如果高维空间中 \(x_i\) 可以由其邻居线性表示,那么在低维空间中对应的 \(y_i\) 也应该保持同样的线性关系。
为每个数据点 \(x_i\) 找到 \(K\) 个最近邻 \(N(i)\)。通过最小化重建误差来计算权重 \(w_{ik}\):
\[\mathcal{E}(W) = \sum_i \left\| x_i - \sum_{j \in N(i)} w_{ij}x_j \right\|^2\]
对于每个点 \(i\),要求 \(\sum_j w_{ij} = 1\)(这保证了对平移和缩放的不变性)。如果 \(j\) 不是 \(i\) 的邻居,则 \(w_{ij}=0\)。这是一个带约束的最小二乘问题。
固定上一步得到的权重 \(W\),寻找低维坐标 \(y_i\),使得在低维空间中的重建误差最小化:
\[\Phi(Y) = \sum_i \left\| y_i - \sum_j w_{ij}y_j \right\|^2\]
该优化问题可以通过求解稀疏矩阵的特征值问题解决。具体来说,涉及矩阵 \(\mathbf{M} = (\mathbf{I} - \mathbf{W})^T (\mathbf{I} - \mathbf{W})\) 的最小非零特征值对应的特征向量。
局部多维缩放(Local MDS)改变了传统MDS算法,传统的 MDS 试图匹配所有点对的距离,这往往受到大距离(远距离点对)的支配。Local MDS 旨在主要保留局部距离(邻居),同时利用排斥力将非邻居推开,以此展开流形。使用如下压力函数:
\[S_L(z_1, \dots, z_N) = \sum_{(i, i') \in \mathcal{N}} (d_{ii'} - ||z_i - z_{i'}||)^2 - \tau \sum_{(i, i') \notin \mathcal{N}} ||z_i - z_{i'}||\]
该函数由两部分的权衡组成:
局部保真项 (Local Fidelity): \(\sum_{(i, i') \in \mathcal{N}} (d_{ii'} - ||z_i - z_{i'}||)^2\)这部分类似于经典的 Stress 函数,但仅针对邻居集合 \(\mathcal{N}\) 求和。它强制要求低维空间中邻居间的距离逼近高维空间中的原始距离 \(d_{ii'}\)。
排斥项 (Repulsion): \(- \tau \sum_{(i, i') \notin \mathcal{N}} ||z_i - z_{i'}||\)针对非邻居点对。由于前面带有负号,最小化总 Stress 意味着这一项的数值越大越好(即 \(||z_i - z_{i'}||\) 越大越好)。



